Backpropagation (BP) 을 구현하기 위해서 알고리즘을 수학적으로 리뷰해보고 python으로 구현하기 위해 정리를 해본다. 이 정리는 다음 웹사이트 (https://medium.com/@14prakash/back-propagation-is-very-simple-who-made-it-complicated-97b794c97e5c)의 내용을 기반으로 작성되었다.
일반적인 neural network의 구조는 다음 그림과 같다.

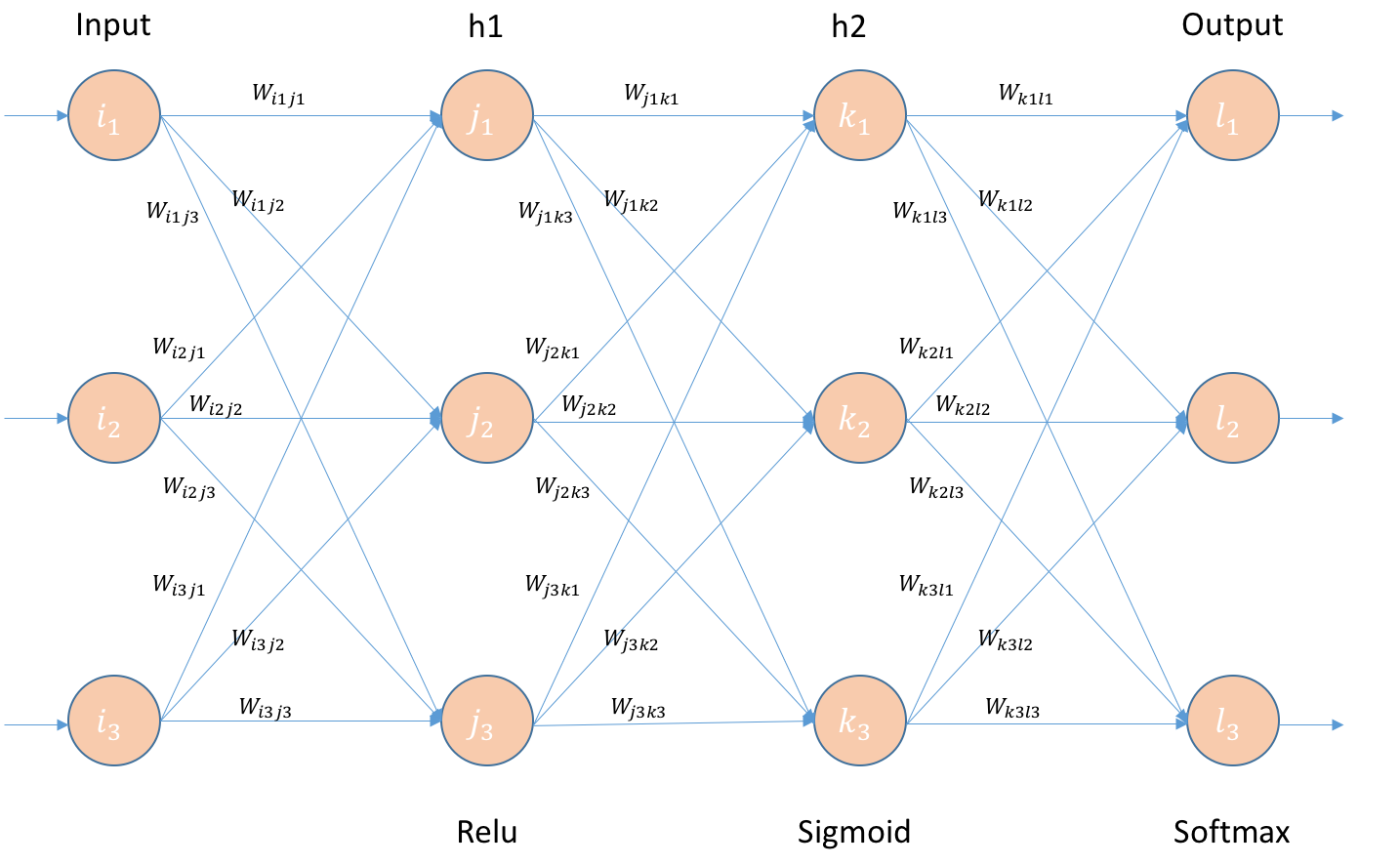
전체적인 알고리즘과 BP의 수식을 유도하기 위해서는 먼저 forward propagation을 살펴보아야 한다. 먼저 input으로부터 첫번째 hidden layer의 input h1_in1을 구하고, activation function (이 예제에서는 첫번째 layer에 ReLU (Rectified Linear Unit)를 사용)을 거쳐 hidden layer의 output h1_out1을 구하는 과정을 살펴보자.

Forward propagation

Layer 1

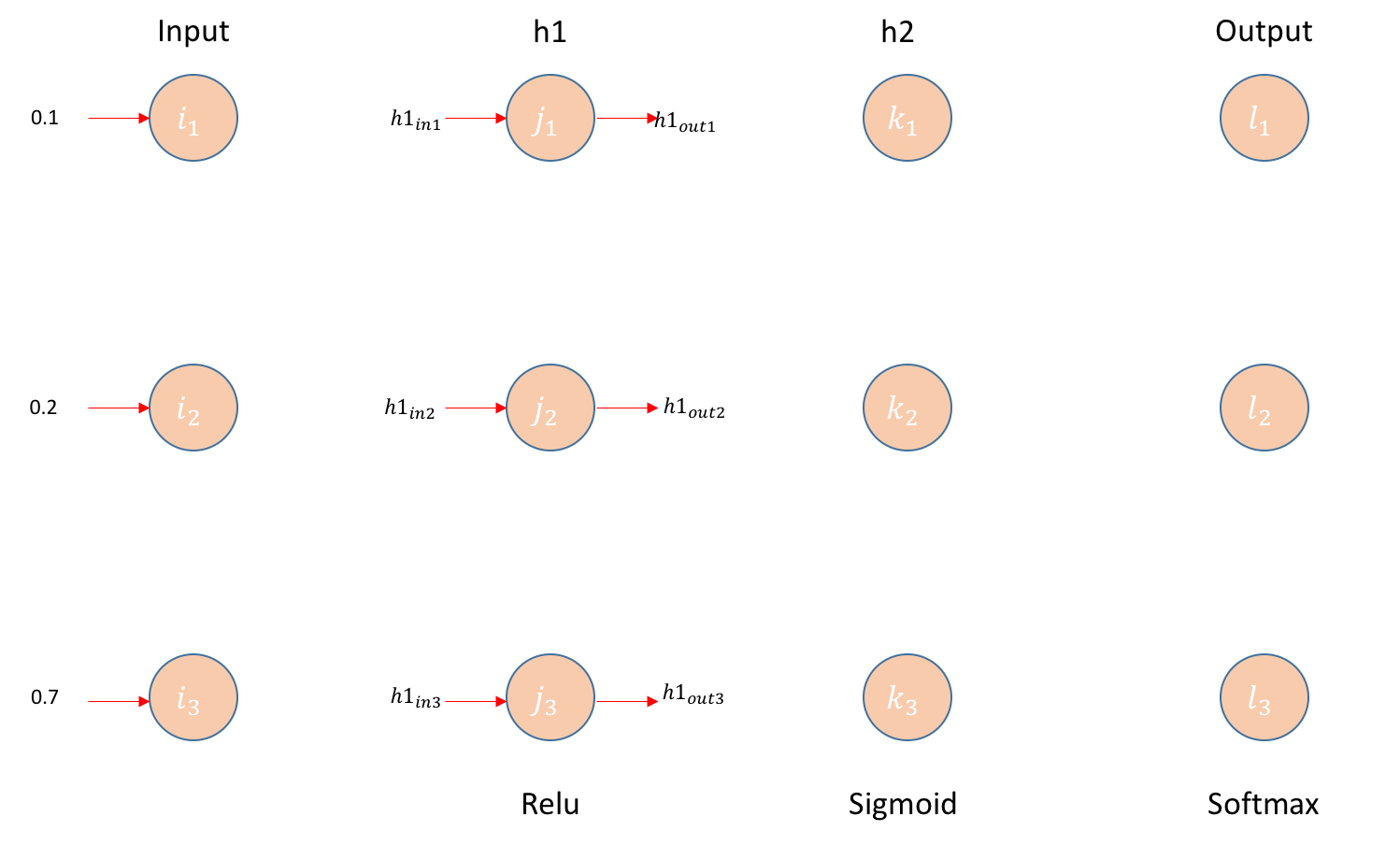
(예제에서) input layer i 에서 첫번째 hidden layer j 로의 weight
$W_{ij} = \begin{bmatrix} w_{i_1j_1} & w_{i_1j_2} & w_{i_1j_3} \\ w_{i_2j_1} & w_{i_2j_2} & w_{i_2j_3} \\ w_{i_3j_1} & w_{i_3j_2} & w_{i_3j_3} \end{bmatrix}$

Hidden layer j 로의 input
$h1_{in_1} = i_1w_{i_1j_1} + i_2w_{i_2j_1} + i_3w_{i_3j_1} + b_{j_1}$
$h1_{in_2} = i_1w_{i_1j_2} + i_2w_{i_2j_2} + i_3w_{i_3j_2} + b_{j_2}$
…

Matrix operation으로 표시하면,
$\begin{bmatrix} h1_{in_1} \\ h1_{in_2} \\ h1_{in_3} \end{bmatrix} = \begin{bmatrix} w_{i_1j_1} & w_{i_2j_1} & w_{i_3j_1} \\ w_{i_1j_2} & w_{i_2j_2} & w_{i_3j_2} \\ w_{i_1j_3} & w_{i_2j_3} & w_{i_3j_3} \end{bmatrix} \begin{bmatrix} i_1 \\ i_2 \\ i_3 \end{bmatrix} + \begin{bmatrix} b_{j_1} \\ b_{j_2} \\ b_{j_3} \end{bmatrix} = W_{ij}^TI + B_j$

ReLU ($=max(0, x)$) operation을 통한 hidden layer j 의 output
$\begin{bmatrix} h1_{out_1} \\ h1_{out_2} \\ h1_{out_3} \end{bmatrix} = \begin{bmatrix} max(0, h1_{in_1}) \\ max(0, h1_{in_2}) \\ max(0, h1_{in_3}) \end{bmatrix}$

Layer 2

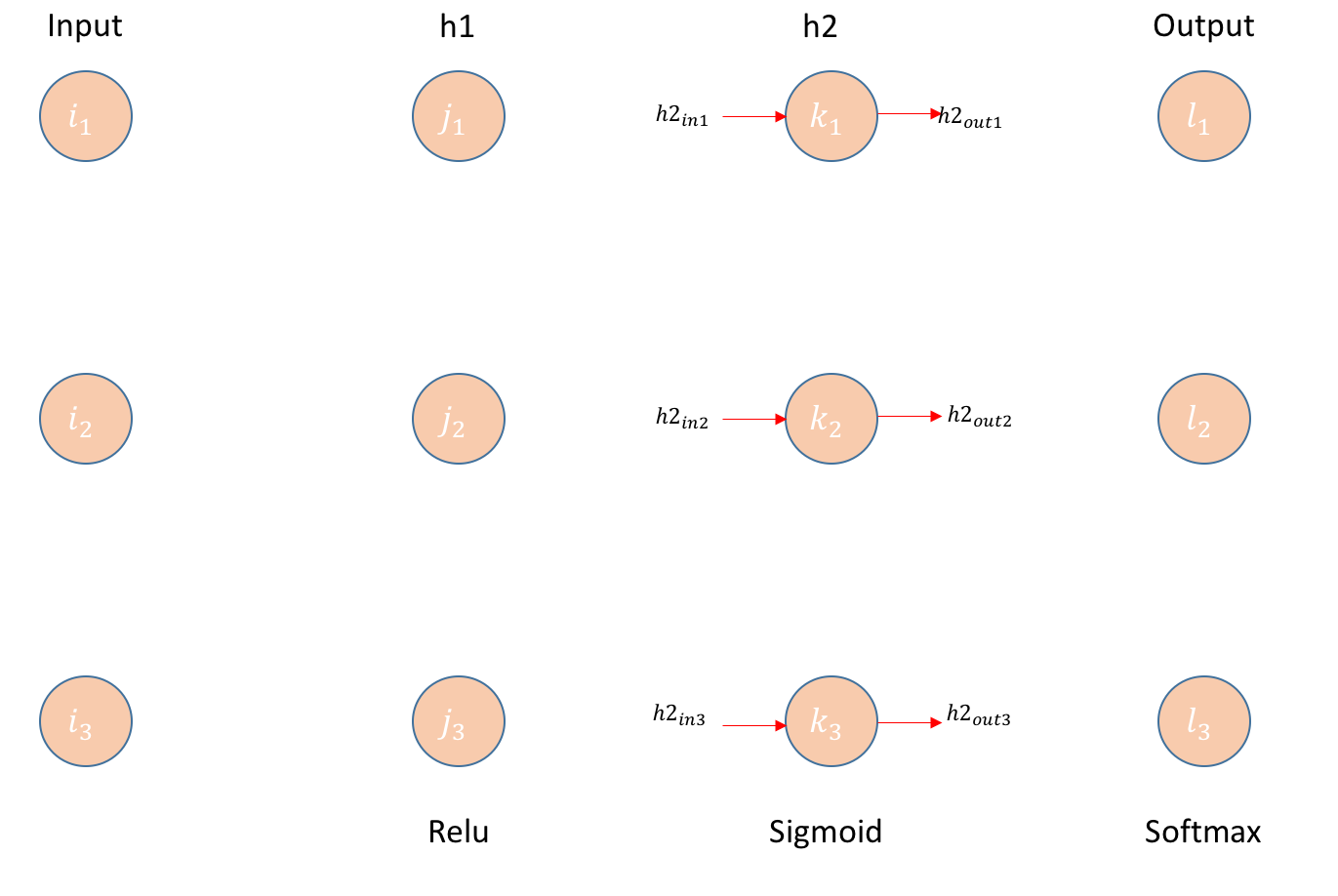
첫번째 hidden layer j 로부터 두번째 hidden layer k 로의 weight
$W_{jk} = \begin{bmatrix} w_{j_1k_1} & w_{j_1k_2} & w_{j_1k_3} \\ w_{j_2k_1} & w_{j_2k_2} & w_{j_2k_3} \\ w_{j_3k_1} & w_{j_3k_2} & w_{j_3k_3} \end{bmatrix}$

Hidden layer k 로의 input
$h2_{in_1} = h1_{out_1}w_{j_1k_1} + h1_{out_2}w_{j_2k_1} + h1_{out_3}w_{j_3k_1} + b_{k_1}$
$h2_{in_2} = h1_{out_1}w_{j_1k_2} + h1_{out_2}w_{j_2k_2} + h1_{out_3}w_{j_3k_2} + b_{k_2}$
…

Matrix operation으로 표시하면,
$\begin{bmatrix} h2_{in_1} \\ h2_{in_2} \\ h2_{in_3} \end{bmatrix} = \begin{bmatrix} w_{j_1k_1} & w_{j_2k_1} & w_{j_3k_1} \\ w_{j_1k_2} & w_{j_2k_2} & w_{j_3k_2} \\ w_{j_1k_3} & w_{j_2k_3} & w_{j_3k_3} \end{bmatrix} \begin{bmatrix} h1_{out_1} \\ h1_{out_2} \\ h1_{out_3} \end{bmatrix} + \begin{bmatrix} b_{k_1} \\ b_{k_2} \\ b_{k_3} \end{bmatrix} = W_{jk}^Th1_{out} + B_k$

Sigmoid ($=1 / (1+e^{-x})$) operation을 통한 hidden layer k 의 output
$\begin{bmatrix} h2_{out_1} \\ h2_{out_2} \\ h2_{out_3} \end{bmatrix} = \begin{bmatrix} 1 / (1 + e^{-h2_{in_1}}) \\ 1 / (1 + e^{-h2_{in_2}}) \\ 1 / (1 + e^{-h2_{in_3}}) \end{bmatrix}$

Layer 3 (output layer)

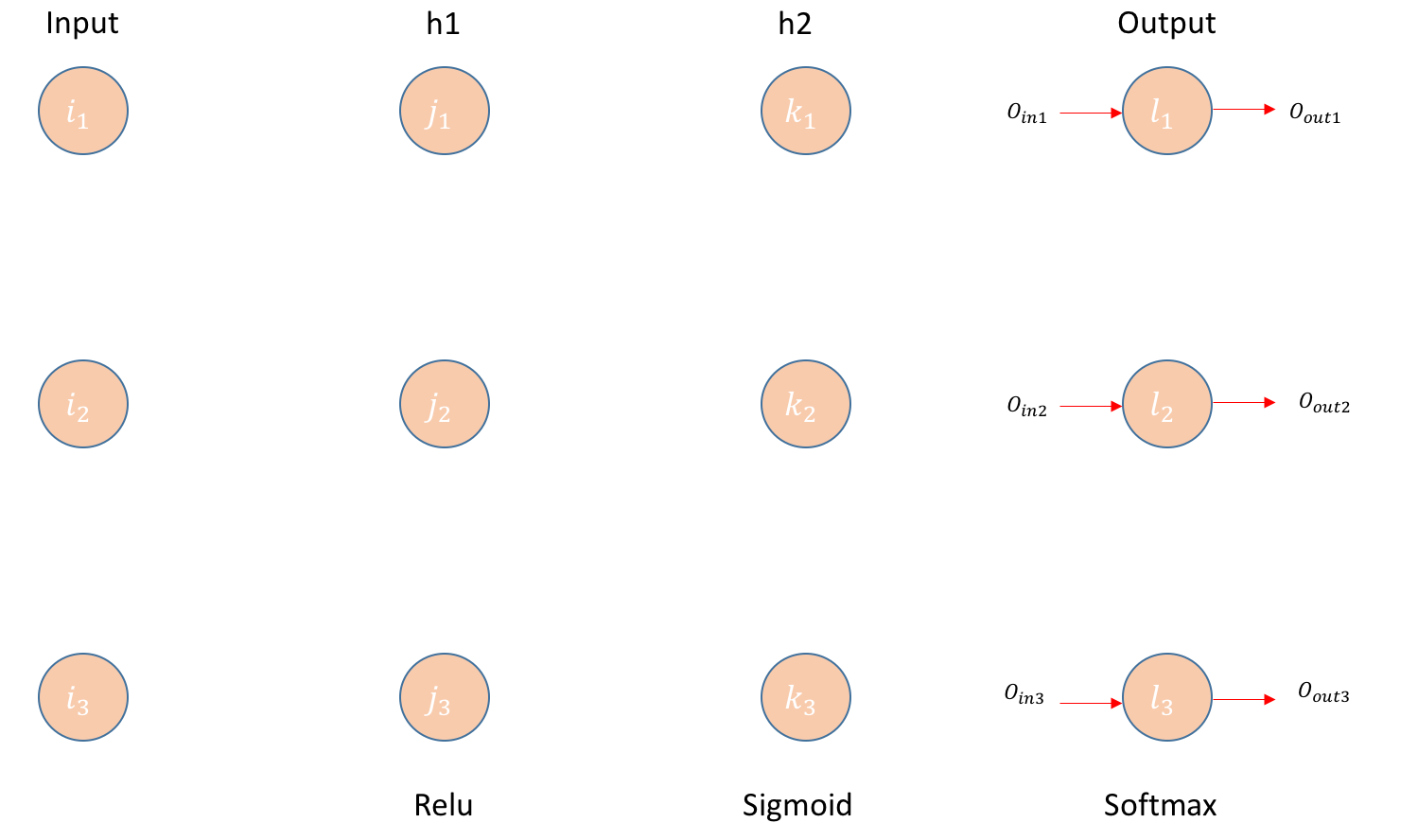
두번째 hidden layer k 로부터 output layer l 로의 weight
$W_{kl} = \begin{bmatrix} w_{k_1l_1} & w_{k_1l_2} & w_{k_1l_3} \\ w_{k_2l_1} & w_{k_2l_2} & w_{k_2l_3} \\ w_{k_3l_1} & w_{k_3l_2} & w_{k_3l_3} \end{bmatrix}$

Output layer l 로의 input
$O_{in_1} = h2_{out_1}w_{k_1l_1} + h2_{out_2}w_{k_2l_1} + h2_{out_3}w_{k_3l_1} + b_{l_1}$
$O_{in_2} = h2_{out_1}w_{k_1l_2} + h2_{out_2}w_{k_2l_2} + h2_{out_3}w_{k_3l_2} + b_{l_2}$
…

Matrix operation으로 표시하면,
$\begin{bmatrix} O_{in_1} \\ O_{in_2} \\ O_{in_3} \end{bmatrix} = \begin{bmatrix} w_{k_1l_1} & w_{k_2l_1} & w_{k_3l_1} \\ w_{k_1l_2} & w_{k_2l_2} & w_{k_3l_2} \\ w_{k_1l_3} & w_{k_2l_3} & w_{k_3l_3} \end{bmatrix} \begin{bmatrix} h2_{out_1} \\ h2_{out_2} \\ h2_{out_3} \end{bmatrix} + \begin{bmatrix} b_{l_1} \\ b_{l_2} \\ b_{l_3} \end{bmatrix} = W_{kl}^Th2_{out} + B_l$

Softmax ($= e^{O_{in_a}} / (\sum_{a = 1}^3 {e^{O_{in_a}}})$) operation을 통한 output layer l 의 output
$\begin{bmatrix} O_{out_1} \\ O_{out_2} \\ O_{out_3} \end{bmatrix} = \begin{bmatrix} e^{O_{in_1}} / (\sum_{a = 1}^3 {e^{O_{in_a}}}) \\ e^{O_{in_2}} / (\sum_{a = 1}^3 {e^{O_{in_a}}}) \\ e^{O_{in_3}} / (\sum_{a = 1}^3 {e^{O_{in_a}}}) \end{bmatrix}$

Error function

여러 가지 error가 사용될 수 있지만, 이 예제에서는 cross-entropy를 사용했다.
$error = -(1/n)(\sum_{i = 1}^n {(y_ilog(O_{out_i}) + (1 - y_i)log(1 - O_{out_i}))}$

Important derivatives

BP는 기본적으로 error의 weight에 대한 변화량을 이용해서 새로운 weight를 구해나가는 gradient descent 방법이고, 그 변화량은 partial derivatives들과 chain rule에 의해서 계산된다. 몇 가지 함수의 derivatives들을 미리 구해놓으면 쉽게 weight에 대한 error의 변화량을 구할 수 있다.

Derivative of Sigmoid

먼저 다음의 미분을 기억하자.
$(1 + e^{-x})' = \frac{d}{dx}(1) + \frac{d}{dx}(e^{-x}) = 0 + (-1)e^{-x}$
Sigmoid의 미분은 다음과 같이 정리할 수 있다.
먼저 $Sigmoid(x) = \theta(x) = \frac{1}{(1 + e^{-x})}$라고 정의하고,
$\frac{d}{dx}\theta(x) = \frac{d}{dx}\frac{1}{(1 + e^{-x})} = \frac{(1)'(1 + e^{-x}) - 1(1 + e^{-x})'}{(1 + e^{-x}) ^ 2} = \frac{e^{-x}}{(1 + e^{-x}) ^ 2}$
$\frac{e^{-x}}{(1 + e^{-x}) ^ 2} = \frac{1}{(1 + e^{-x})}\cdot\frac{e^{-x}}{(1 + e^{-x})} = \frac{1}{(1 + e^{-x})}\cdot(1 - \frac{1}{(1 + e^{-x})})$
$\therefore \frac{d}{dx}\theta(x) = \theta(x)\cdot(1 - \theta(x))$

Derivative of ReLU

$ReLU(x) = max(0, x)$
$x > 0$ 인 경우, $\frac{d}{dx}ReLU(x) = \frac{d}{dx}(x) = 1$
그 외의 경우, $\frac{d}{dx}ReLU(x) = \frac{d}{dx}(0) = 0$

Derivative of Softmax

Softmax는 probability를 표현할 때 주로 사용되므로 $Softmax(x_i) = p(x_i)$라고 정의하자.
$\frac{d}{dx_i}p(x_i) = \frac{d}{dx_i}(\frac{e^{x_i}}{e^{x_1} + e^{x_2} +\cdots+ e^{x_n}}) = \frac{d}{dx_i}(\frac{e^{x_i}}{\sum_{j = 1}^{n} {e^{x_j}}})$
$= \frac{(e^{x_i})'(\sum_{j = 1}^{n} {e^{x_j}}) - (e^{x_i})(\sum_{j = 1}^{n} {e^{x_j}})'}{(\sum_{j = 1}^{n} {e^{x_j}})^2} = \frac{e^{x_i}(\sum_{j = 1}^{n} {e^{x_j}}) - (e^{x_i})(e^{x_i})}{(\sum_{j = 1}^{n} {e^{x_j}})^2}$
$= \frac{e^{x_i}(\sum_{j = 1}^{n} {e^{x_j}} - e^{x_i})}{(\sum_{j = 1}^{n} {e^{x_j}})^2} = \frac{e^{x_i}}{\sum_{j = 1}^{n} {e^{x_j}}}\frac{(\sum_{j = 1}^{n} {e^{x_j}} - e^{x_i})}{\sum_{j = 1}^{n} {e^{x_j}}}$
$= \frac{e^{x_i}}{\sum_{j = 1}^{n} {e^{x_j}}}\left(1 - \frac{e^{x_i}}{\sum_{j = 1}^{n} {e^{x_j}}}\right) = p(x_i)(1 - p(x_i))$

Backpropagation

Backpropagating error between output layer and hidden layer k

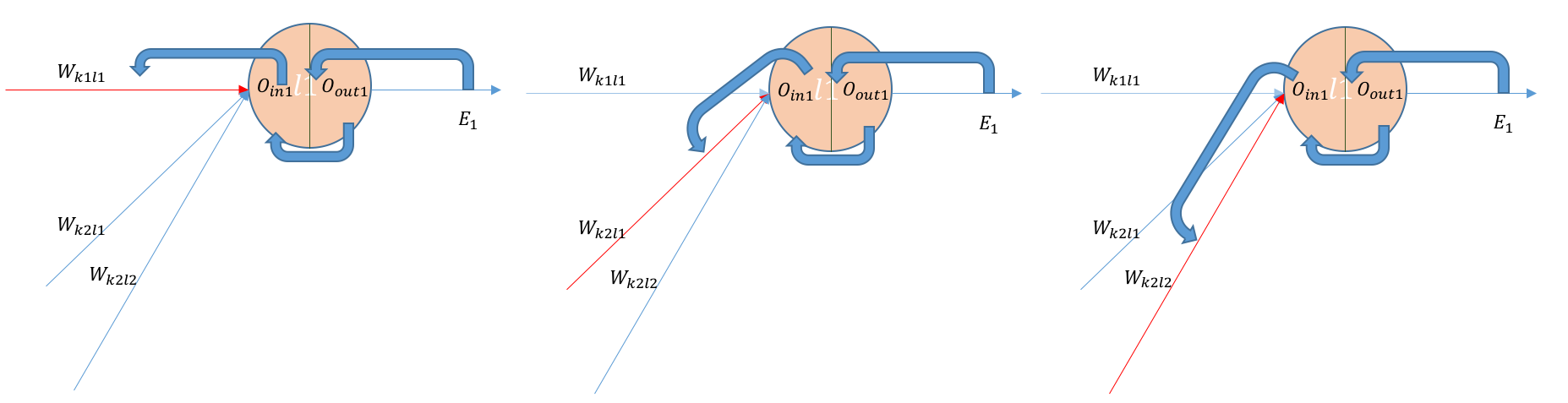
위의 그림에서 맨 오른쪽의 빨간 화살표로 표시된 weight는 $w_{k_3l_1}$ 이어야 한다 (그림에 오류가 있음).

Output layer와 그 직전 hidden layer 사이의 weight (즉 $W_{kl}$ matrix의 원소들, 예를 들면 $w_{k_1l_1}$)가 error에 미치는 영향은 $\frac{\partial{E}}{\partial{w_{k_1l_1}}}$ 로 계산할 수 있는데, 위의 그림에서 보듯이 크게 세 단계를 거치는 chain rule로 표시할 수 있다.
$\frac{\partial{E}}{\partial{w_{k_1l_1}}} = \frac{\partial{E}}{\partial{O_{out_1}}}\cdot\frac{\partial{O_{out_1}}}{\partial{O_{in_1}}}\cdot\frac{\partial{O_{in_1}}}{\partial{w_{k_1l_1}}}$

각각의 미분값을 살펴보도록 하자.

첫번째 미분값은,

$\frac{\partial{E}}{\partial{O_{out_1}}} = \frac{\partial{E_1}}{\partial{O_{out_1}}}$ ($O_{out_1}$은 $E_1$에만 기여를 하므로)
$\frac{\partial}{\partial{O_{out_1}}}-(y_1log(O_{out_1}) + (1 - y_1)log(1 - O_{out_1}))$
$= -y_1\frac{d(log(O_{out_1}))}{dO_{out_1}} - (1 - y_1)\frac{d(log(1 - O_{out_1}))}{dO_{out_1}}$
$= -y_1\cdot\frac{1}{O_{out_1}} - (1 - y_1)\cdot(-\frac{1}{(1 - O_{out_1})}) = - \frac{y_1}{O_{out_1}} + \frac{(1 - y_1)}{(1 - O_{out_1})}$

Matrix operation으로 표시하면,
$\begin{bmatrix} \frac{\partial{E_1}}{\partial{O_{out1}}} \\ \frac{\partial{E_2}}{\partial{O_{out2}}} \\ \frac{\partial{E_3}}{\partial{O_{out3}}} \end{bmatrix} = \begin{bmatrix} -\frac{y_1}{O_{out_1}} + \frac{(1 - y_1)}{(1 - O_{out_1})} \\ -\frac{y_2}{O_{out_2}} + \frac{(1 - y_2)}{(1 - O_{out_2})} \\ -\frac{y_3}{O_{out_3}} + \frac{(1 - y_3)}{(1 - O_{out_3})} \end{bmatrix}$

두번째 미분값을 살펴보면,
$\frac{\partial{O_{out_1}}}{\partial{O_{in_1}}} = \frac{\partial}{\partial{O_{in_1}}}softmax(O_{in_1}) = \frac{\partial}{\partial{O_{in_1}}}(e^{O_{in_1}} / (\sum_{a = 1}^3 {e^{O_{in_a}}}))$
$=\frac{e^{O_{in_1}}(e^{O_{in_2}} + e^{O_{in_3}})}{(e^{O_{in_1}} + e^{O_{in_2}} + e^{O_{in_3}}) ^ 2}$ (위에서 미리 구했던 softmax의 미분 참조)

Matrix operation으로 표시하면, $\begin{bmatrix} \frac{\partial{O_{out_1}}}{\partial{O_{in_1}}} \\ \frac{\partial{O_{out_2}}}{\partial{O_{in_2}}} \\ \frac{\partial{O_{out_3}}}{\partial{O_{in_3}}} \end{bmatrix} = \begin{bmatrix} \frac{e^{O_{in_1}}(e^{O_{in_2}} + e^{O_{in_3}})}{(e^{O_{in_1}} + e^{O_{in_2}} + e^{O_{in_3}}) ^ 2} \\ \frac{e^{O_{in_2}}(e^{O_{in_1}} + e^{O_{in_3}})}{(e^{O_{in_1}} + e^{O_{in_2}} + e^{O_{in_3}}) ^ 2} \\ \frac{e^{O_{in_3}}(e^{O_{in_1}} + e^{O_{in_2}})}{(e^{O_{in_1}} + e^{O_{in_2}} + e^{O_{in_3}}) ^ 2} \end{bmatrix}$

세번째 미분값은,
$\frac{\partial{O_{in1}}}{\partial{w_{k_1l_1}}} = \frac{\partial}{\partial{w_{k_1l_1}}}(h2_{out1}w_{k_1l_1} + h2_{out2}w_{k_2l_1} + h2_{out3}w_{k_3l_1} + b_{l_1}) = h2_{out1}$
$O_{in1}$에 기여하는 weight들은 $w_{k_\cdot l_1}$ 이므로 다음과 같은 matrix operation으로 표현할 수 있다.
$\begin{bmatrix} \frac{\partial{O_{in1}}}{\partial{w_{k_1l_1}}} \\ \frac{\partial{O_{in1}}}{\partial{w_{k_2l_1}}} \\ \frac{\partial{O_{in1}}}{\partial{w_{k_3l_1}}} \end{bmatrix} = \begin{bmatrix} h2_{out1} \\ h2_{out2} \\ h2_{out3} \end{bmatrix}$

마찬가지로 $O_{in2}$와 $O_{in3}$에 기여하는 weight들은 각각 $w_{k_\cdot l_2}$, $w_{k_\cdot l_3}$ 이므로,
$\begin{bmatrix} \frac{\partial{O_{in2}}}{\partial{w_{k_1l_2}}} \\ \frac{\partial{O_{in2}}}{\partial{w_{k_2l_2}}} \\ \frac{\partial{O_{in2}}}{\partial{w_{k_3l_2}}} \end{bmatrix} = \begin{bmatrix} h2_{out1} \\ h2_{out2} \\ h2_{out3} \end{bmatrix}, \begin{bmatrix} \frac{\partial{O_{in3}}}{\partial{w_{k_1l_3}}} \\ \frac{\partial{O_{in3}}}{\partial{w_{k_2l_3}}} \\ \frac{\partial{O_{in3}}}{\partial{w_{k_3l_3}}} \end{bmatrix} = \begin{bmatrix} h2_{out1} \\ h2_{out2} \\ h2_{out3} \end{bmatrix}$

$W_{kl}$ matrix에 대해서 확대해보면,
$\begin{bmatrix} \frac{\partial{O_{in1}}}{\partial{w_{k_1l_1}}} & \frac{\partial{O_{in2}}}{\partial{w_{k_1l_2}}} & \frac{\partial{O_{in3}}}{\partial{w_{k_1l_3}}}\\ \frac{\partial{O_{in1}}}{\partial{w_{k_2l_1}}} & \frac{\partial{O_{in2}}}{\partial{w_{k_2l_2}}} & \frac{\partial{O_{in3}}}{\partial{w_{k_2l_3}}}\\ \frac{\partial{O_{in1}}}{\partial{w_{k_3l_1}}} & \frac{\partial{O_{in2}}}{\partial{w_{k_3l_2}}} & \frac{\partial{O_{in3}}}{\partial{w_{k_3l_3}}} \end{bmatrix} = \begin{bmatrix} h2_{out1} & h2_{out1} & h2_{out1} \\ h2_{out2} & h2_{out2} & h2_{out2} \\ h2_{out3} & h2_{out3} & h2_{out3} \end{bmatrix}$

위의 그림을 다시 한번 상기하면서 $W_{kj}$에 대한 error의 미분값을 정리해보자.
$w_{k_1l_1}$은 $E_1$에만 기여를 하므로 $\frac{\partial{E}}{\partial{w_{k_1l_1}}} = \frac{\partial{E_1}}{\partial{w_{k_1l_1}}}$이 되고, $w_{k_1l_2}$은 $E_2$에만 기여를 하므로 $\frac{\partial{E}}{\partial{w_{k_1l_2}}} = \frac{\partial{E_2}}{\partial{w_{k_1l_1}}}$가 된다.
일반화를 시켜보면

$\delta{W_{kl}} = \begin{bmatrix} \frac{\partial{E}}{\partial{w_{k_1l_1}}} & \frac{\partial{E}}{\partial{w_{k_1l_2}}} & \frac{\partial{E}}{\partial{w_{k_1l_3}}} \\ \frac{\partial{E}}{\partial{w_{k_2l_1}}} & \frac{\partial{E}}{\partial{w_{k_2l_2}}} & \frac{\partial{E}}{\partial{w_{k_2l_3}}} \\ \frac{\partial{E}}{\partial{w_{k_3l_1}}} & \frac{\partial{E}}{\partial{w_{k_3l_2}}} & \frac{\partial{E}}{\partial{w_{k_3l_3}}} \end{bmatrix} = \begin{bmatrix} \frac{\partial{E_1}}{\partial{w_{k_1l_1}}} & \frac{\partial{E_2}}{\partial{w_{k_1l_2}}} & \frac{\partial{E_3}}{\partial{w_{k_1l_3}}} \\ \frac{\partial{E_1}}{\partial{w_{k_2l_1}}} & \frac{\partial{E_2}}{\partial{w_{k_2l_2}}} & \frac{\partial{E_3}}{\partial{w_{k_2l_3}}} \\ \frac{\partial{E_1}}{\partial{w_{k_3l_1}}} & \frac{\partial{E_2}}{\partial{w_{k_3l_2}}} & \frac{\partial{E_3}}{\partial{w_{k_3l_3}}} \end{bmatrix}$
$= \begin{bmatrix} \frac{\partial{E_1}}{\partial{O_{out_1}}}\frac{\partial{O_{out_1}}}{\partial{O_{in_1}}}\frac{\partial{O_{in_1}}}{\partial{w_{k_1l_1}}} & \frac{\partial{E_2}}{\partial{O_{out_2}}}\frac{\partial{O_{out_2}}}{\partial{O_{in_2}}}\frac{\partial{O_{in_2}}}{\partial{w_{k_1l_2}}} & \frac{\partial{E_3}}{\partial{O_{out_3}}}\frac{\partial{O_{out_3}}}{\partial{O_{in_3}}}\frac{\partial{O_{in_3}}}{\partial{w_{k_1l_3}}} \\ \frac{\partial{E_1}}{\partial{O_{out_1}}}\frac{\partial{O_{out_1}}}{\partial{O_{in_1}}}\frac{\partial{O_{in_1}}}{\partial{w_{k_2l_1}}} & \frac{\partial{E_2}}{\partial{O_{out_2}}}\frac{\partial{O_{out_2}}}{\partial{O_{in_2}}}\frac{\partial{O_{in_2}}}{\partial{w_{k_2l_2}}} & \frac{\partial{E_3}}{\partial{O_{out_3}}}\frac{\partial{O_{out_3}}}{\partial{O_{in_3}}}\frac{\partial{O_{in_3}}}{\partial{w_{k_2l_3}}} \\ \frac{\partial{E_1}}{\partial{O_{out_1}}}\frac{\partial{O_{out_1}}}{\partial{O_{in_1}}}\frac{\partial{O_{in_1}}}{\partial{w_{k_3l_1}}} & \frac{\partial{E_2}}{\partial{O_{out_2}}}\frac{\partial{O_{out_2}}}{\partial{O_{in_2}}}\frac{\partial{O_{in_2}}}{\partial{w_{k_3l_2}}} & \frac{\partial{E_3}}{\partial{O_{out_3}}}\frac{\partial{O_{out_3}}}{\partial{O_{in_3}}}\frac{\partial{O_{in_3}}}{\partial{w_{k_3l_3}}} \end{bmatrix}$
$= \begin{bmatrix} \frac{\partial{E_1}}{\partial{O_{out_1}}} & \frac{\partial{E_2}}{\partial{O_{out_2}}} & \frac{\partial{E_3}}{\partial{O_{out_3}}} \\ \frac{\partial{E_1}}{\partial{O_{out_1}}} & \frac{\partial{E_2}}{\partial{O_{out_2}}} & \frac{\partial{E_3}}{\partial{O_{out_3}}} \\ \frac{\partial{E_1}}{\partial{O_{out_1}}} & \frac{\partial{E_2}}{\partial{O_{out_2}}} & \frac{\partial{E_3}}{\partial{O_{out_3}}} \end{bmatrix} \ast \begin{bmatrix} \frac{\partial{O_{out_1}}}{\partial{O_{in_1}}} & \frac{\partial{O_{out_2}}}{\partial{O_{in_2}}} & \frac{\partial{O_{out_3}}}{\partial{O_{in_3}}} \\ \frac{\partial{O_{out_1}}}{\partial{O_{in_1}}} & \frac{\partial{O_{out_2}}}{\partial{O_{in_2}}} & \frac{\partial{O_{out_3}}}{\partial{O_{in_3}}} \\ \frac{\partial{O_{out_1}}}{\partial{O_{in_1}}} & \frac{\partial{O_{out_2}}}{\partial{O_{in_2}}} & \frac{\partial{O_{out_3}}}{\partial{O_{in_3}}} \end{bmatrix} \ast \begin{bmatrix} \frac{\partial{O_{in_1}}}{\partial{w_{k_1l_1}}} & \frac{\partial{O_{in_2}}}{\partial{w_{k_1l_2}}} & \frac{\partial{O_{in_3}}}{\partial{w_{k_1l_3}}} \\ \frac{\partial{O_{in_1}}}{\partial{w_{k_2l_1}}} & \frac{\partial{O_{in_2}}}{\partial{w_{k_2l_2}}} & \frac{\partial{O_{in_3}}}{\partial{w_{k_2l_3}}} \\ \frac{\partial{O_{in_1}}}{\partial{w_{k_3l_1}}} & \frac{\partial{O_{in_2}}}{\partial{w_{k_3l_2}}} & \frac{\partial{O_{in_3}}}{\partial{w_{k_3l_3}}} \end{bmatrix}$
Operator *는 element-wise product를 나타낸다.

새로운 weight는 learning rate, $\alpha$와 위에서 구한 gradient $\delta{W_{kl}}$에 의해서 구할 수 있다. $W_{kl}^{new} = W_{kl} - \alpha\cdot\delta{W_{kl}}$

Backpropagating error between hidden layer j and k

한단계 더 뒤로 가서 hidden layer j와 k 사이에서의 backpropagation을 알아보도록 하자.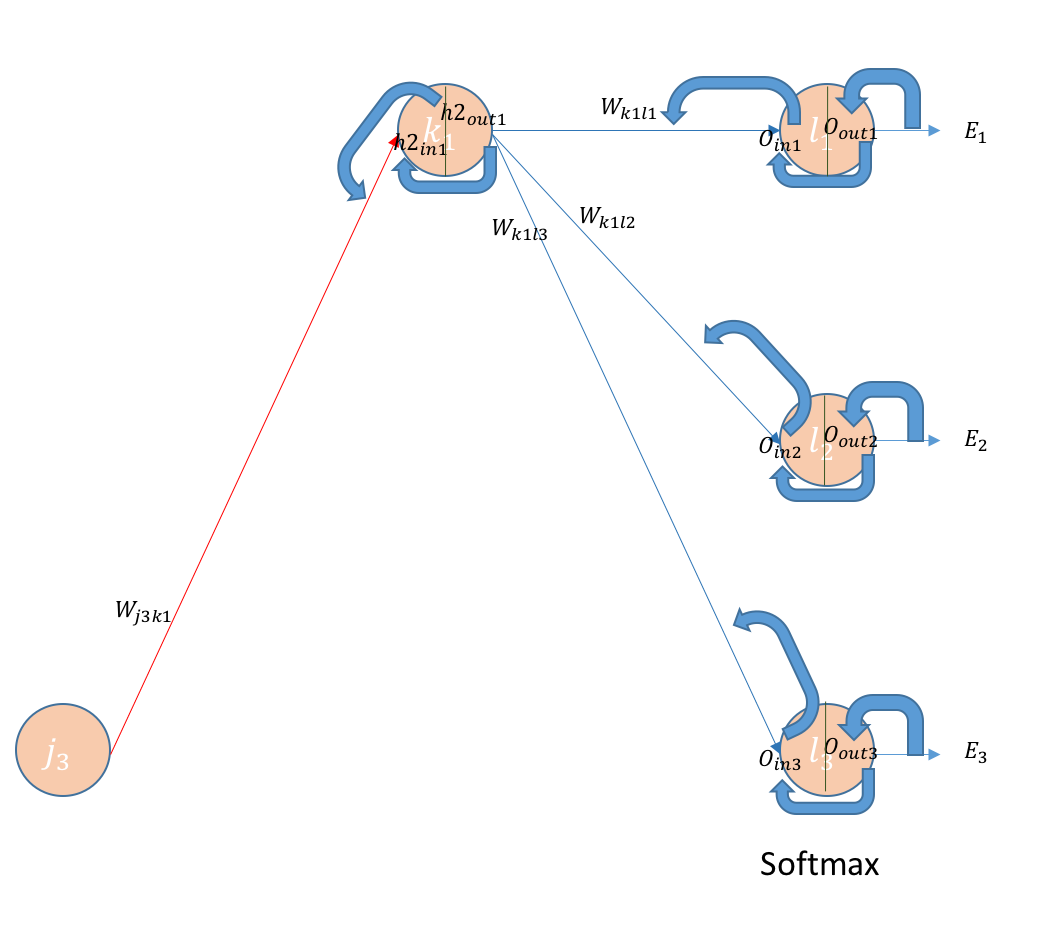

위에서와 마찬가지로 $w_{j_1k_1}$의 error에 대한 변화량 $\frac{\partial{E}}{\partial{w_{j_1k_1}}}$은 chain rule에 의해서 다음과 같이 나타낼 수 있다.
$\frac{\partial{E}}{\partial{w_{j_1k_1}}} = \frac{\partial{E}}{\partial{h2_{out_1}}} \cdot \frac{\partial{h2_{out_1}}}{\partial{h2_{in_1}}} \cdot \frac{\partial{h2_{in_1}}}{\partial{w_{j_1k_1}}}$

첫번째, $h2_{in_1}$ 과 $h2_{out_1}$ 사이의 관계는 sigmoid 함수로 표현되고, 그 미분식은 위에서 미리 유도되었다. $\frac{\partial{h2_{out_1}}}{\partial{h2_{in_1}}} = \frac{\partial}{\partial{h2_{in_1}}} (sigmoid(h2_{in_1})) = sigmoid(h2_{in_1})\cdot(1 - sigmoid(h2_{in_1}))$

Matrix operation으로 표현하면, $\begin{bmatrix} \frac{\partial{h2_{out_1}}}{\partial{h2_{in_1}}} \\ \frac{\partial{h2_{out_2}}}{\partial{h2_{in_2}}} \\ \frac{\partial{h2_{out_3}}}{\partial{h2_{in_3}}} \end{bmatrix} = \begin{bmatrix} sigmoid(h2_{in_1})\cdot(1 - sigmoid(h2_{in_1})) \\ sigmoid(h2_{in_2})\cdot(1 - sigmoid(h2_{in_2})) \\ sigmoid(h2_{in_3})\cdot(1 - sigmoid(h2_{in_3})) \end{bmatrix}$

두번째, $w_{j_1k_1}$와 $h2_{in_1}$과의 관계는 간단하게 다음과 같이 표현된다. $\frac{\partial{h2_{in_1}}}{\partial{w_{j_1k_1}}} = \frac{\partial}{\partial{w_{j_1k_1}}}(h1_{out1}w_{j_1k_1} + h1_{out2}w_{j_2k_1} + h1_{out3}w_{j_3k_1} + b_{k_1}) = h1_{out1}$

Weight $w_{j\cdot k_1}, w_{j\cdot k_2}, w_{j\cdot k_3}$은 각각 $h2_{in_1}, h2_{in_2}, h2_{in_3}$ 에만 기여하므로 matrix operation으로 표현하면,
$\begin{bmatrix} \frac{\partial{h2_{in1}}}{\partial{w_{j_1k1}}} & \frac{\partial{h2_{in2}}}{\partial{w_{j_1k_2}}} & \frac{\partial{h2_{in3}}}{\partial{w_{j_1k_3}}}\\ \frac{\partial{h2_{in1}}}{\partial{w_{j_2k1}}} & \frac{\partial{h2_{in2}}}{\partial{w_{j_2k_2}}} & \frac{\partial{h2_{in3}}}{\partial{w_{j_2k_3}}}\\ \frac{\partial{h2_{in1}}}{\partial{w_{j_3k1}}} & \frac{\partial{h2_{in2}}}{\partial{w_{j_3k_2}}} & \frac{\partial{h2_{in3}}}{\partial{w_{j_3k_3}}} \end{bmatrix} = \begin{bmatrix} h1_{out1} & h1_{out1} & h1_{out1} \\ h1_{out2} & h1_{out2} & h1_{out2} \\ h1_{out3} & h1_{out3} & h1_{out3} \end{bmatrix}$

세번째 $\frac{\partial{E}}{\partial{h2_{out_1}}}$ 는 조금 복잡한데 $h2_{out_1}$ 이 모든 error, 즉 $E_1$, $E_2$, $E_3$ 에 모두 기여를 하기 때문이다.
$\frac{\partial{E}}{\partial{h2_{out_1}}} = \frac{\partial{(E_1 + E_2 + E_3)}}{\partial{h2_{out_1}}} = \frac{\partial{E_1}}{\partial{h2_{out_1}}} + \frac{\partial{E_2}}{\partial{h2_{out_1}}} + \frac{\partial{E_3}}{\partial{h2_{out_1}}}$

각각의 미분값을 정리해보면 다음과 같다.
$\frac{\partial{E_1}}{\partial{h2_{out_1}}} = \frac{\partial{E_1}}{\partial{O_{out_1}}} \cdot \frac{\partial{O_{out_1}}}{\partial{O_{in_1}}} \cdot \frac{\partial{O_{in_1}}}{\partial{h2_{out_1}}}$
$\frac{\partial{E_2}}{\partial{h2_{out_1}}} = \frac{\partial{E_2}}{\partial{O_{out_2}}} \cdot \frac{\partial{O_{out_2}}}{\partial{O_{in_2}}} \cdot \frac{\partial{O_{in_2}}}{\partial{h2_{out_1}}}$
$\frac{\partial{E_3}}{\partial{h2_{out_1}}} = \frac{\partial{E_3}}{\partial{O_{out_3}}} \cdot \frac{\partial{O_{out_3}}}{\partial{O_{in_3}}} \cdot \frac{\partial{O_{in_3}}}{\partial{h2_{out_1}}}$

Matrix operation으로 표현해보면,
$\begin{bmatrix} \frac{\partial{E}}{\partial{h2_{out_1}}} \\ \frac{\partial{E}}{\partial{h2_{out_2}}} \\ \frac{\partial{E}}{\partial{h2_{out_3}}} \end{bmatrix} = \begin{bmatrix} \frac{\partial{E_1}}{\partial{h2_{out_1}}} + \frac{\partial{E_2}}{\partial{h2_{out_1}}} + \frac{\partial{E_3}}{\partial{h2_{out_1}}} \\ \frac{\partial{E_1}}{\partial{h2_{out_2}}} + \frac{\partial{E_2}}{\partial{h2_{out_2}}} + \frac{\partial{E_3}}{\partial{h2_{out_2}}} \\ \frac{\partial{E_1}}{\partial{h2_{out_3}}} + \frac{\partial{E_2}}{\partial{h2_{out_3}}} + \frac{\partial{E_3}}{\partial{h2_{out_3}}} \end{bmatrix}$
$= \begin{bmatrix} \frac{\partial{E_1}}{\partial{O_{out_1}}} \frac{\partial{O_{out_1}}}{\partial{O_{in_1}}} \frac{\partial{O_{in_1}}}{\partial{h2_{out_1}}} + \frac{\partial{E_2}}{\partial{O_{out_2}}} \frac{\partial{O_{out_2}}}{\partial{O_{in_2}}} \frac{\partial{O_{in_2}}}{\partial{h2_{out_1}}} + \frac{\partial{E_3}}{\partial{O_{out_3}}} \frac{\partial{O_{out_3}}}{\partial{O_{in_3}}} \frac{\partial{O_{in_3}}}{\partial{h2_{out_1}}} \\ \frac{\partial{E_1}}{\partial{O_{out_1}}} \frac{\partial{O_{out_1}}}{\partial{O_{in_1}}} \frac{\partial{O_{in_1}}}{\partial{h2_{out_2}}} + \frac{\partial{E_2}}{\partial{O_{out_2}}} \frac{\partial{O_{out_2}}}{\partial{O_{in_2}}} \frac{\partial{O_{in_2}}}{\partial{h2_{out_2}}} + \frac{\partial{E_3}}{\partial{O_{out_3}}} \frac{\partial{O_{out_3}}}{\partial{O_{in_3}}} \frac{\partial{O_{in_3}}}{\partial{h2_{out_2}}} \\ \frac{\partial{E_1}}{\partial{O_{out_1}}} \frac{\partial{O_{out_1}}}{\partial{O_{in_1}}} \frac{\partial{O_{in_1}}}{\partial{h2_{out_3}}} + \frac{\partial{E_2}}{\partial{O_{out_2}}} \frac{\partial{O_{out_2}}}{\partial{O_{in_2}}} \frac{\partial{O_{in_2}}}{\partial{h2_{out_3}}} + \frac{\partial{E_3}}{\partial{O_{out_3}}} \frac{\partial{O_{out_3}}}{\partial{O_{in_3}}} \frac{\partial{O_{in_3}}}{\partial{h2_{out_3}}} \end{bmatrix}$

위의 식을 잘 살펴보면 $\frac{\partial{E_1}}{\partial{O_{out_1}}} \frac{\partial{O_{out_1}}}{\partial{O_{in_1}}}$은 output layer와 hidden layer k 사이의 backpropagation을 계산할 때 이미 구해놓은 값이라는 것을 알 수 있다. 따라서 $\frac{\partial{O_{in_1}}}{\partial{h2_{out_1}}}$만 유도하면 된다. $O_{in_1}, O_{in_2}$등은 다음과 같이 표현되므로,
$O_{in_1} = h2_{out_1}w_{k_1l_1} + h2_{out_2}w_{k_2l_1} + h2_{out_3}w_{k_3l_1} + b_{l_1}$
$O_{in_2} = h2_{out_1}w_{k_1l_2} + h2_{out_2}w_{k_2l_2} + h2_{out_3}w_{k_3l_2} + b_{l_2}$
$...$

$\frac{\partial{O_{in_\cdot}}}{\partial{h2_{out_\cdot}}}$ 은 다음과 같이 표현된다.
$\begin{bmatrix} \frac{\partial{O_{in_1}}}{\partial{h2_{out_1}}} & \frac{\partial{O_{in_2}}}{\partial{h2_{out_1}}} & \frac{\partial{O_{in_3}}}{\partial{h2_{out_1}}} \\ \frac{\partial{O_{in_1}}}{\partial{h2_{out_2}}} & \frac{\partial{O_{in_2}}}{\partial{h2_{out_2}}} & \frac{\partial{O_{in_3}}}{\partial{h2_{out_2}}} \\ \frac{\partial{O_{in_1}}}{\partial{h2_{out_3}}} & \frac{\partial{O_{in_2}}}{\partial{h2_{out_3}}} & \frac{\partial{O_{in_3}}}{\partial{h2_{out_3}}} \end{bmatrix} = \begin{bmatrix} w_{k_1l_1} & w_{k_1l_2} & w_{k_1l_3} \\ w_{k_2l_1} & w_{k_2l_2} & w_{k_2l_3} \\ w_{k_3l_1} & w_{k_3l_2} & w_{k_3l_3} \end{bmatrix}$

정리해보면, 다음과 같은 matrix operation을 통해서 $\frac{\partial{E}}{\partial{h2_{out_\cdot}}}$을 구할 수 있다.
$\begin{bmatrix} \frac{\partial{E}}{\partial{h2_{out_1}}} \\ \frac{\partial{E}}{\partial{h2_{out_2}}} \\ \frac{\partial{E}}{\partial{h2_{out_3}}} \end{bmatrix} = \begin{bmatrix} w_{k_1l_1} & w_{k_1l_2} & w_{k_1l_3} \\ w_{k_2l_1} & w_{k_2l_2} & w_{k_2l_3} \\ w_{k_3l_1} & w_{k_3l_2} & w_{k_3l_3} \end{bmatrix} \cdot \left ( \begin{bmatrix} \frac{\partial{E_1}}{\partial{O_{out_1}}} \\ \frac{\partial{E_2}}{\partial{O_{out_2}}} \\ \frac{\partial{E_3}}{\partial{O_{out_3}}} \end{bmatrix} \ast \begin{bmatrix} \frac{\partial{O_{out_1}}}{\partial{O_{in_1}}} \\ \frac{\partial{O_{out_2}}}{\partial{O_{in_2}}} \\ \frac{\partial{O_{out_3}}}{\partial{O_{in_3}}} \end{bmatrix} \right )$

최종적으로 구하고자 하는 matrix는
$\delta{W_{jk}} = \begin{bmatrix} \frac{\partial{E}}{\partial{w_{j_1k_1}}} & \frac{\partial{E}}{\partial{w_{j_1k_2}}} & \frac{\partial{E}}{\partial{w_{j_1k_3}}} \\ \frac{\partial{E}}{\partial{w_{j_2k_1}}} & \frac{\partial{E}}{\partial{w_{j_2k_2}}} & \frac{\partial{E}}{\partial{w_{j_2k_3}}} \\ \frac{\partial{E}}{\partial{w_{j_3k_1}}} & \frac{\partial{E}}{\partial{w_{j_3k_2}}} & \frac{\partial{E}}{\partial{w_{j_3k_3}}} \end{bmatrix}$
$= \begin{bmatrix} \frac{\partial{E}}{\partial{h2_{out_1}}}\frac{\partial{h2_{out_1}}}{\partial{h2_{in_1}}}\frac{\partial{h2_{in_1}}}{\partial{w_{j_1k_1}}} & \frac{\partial{E}}{\partial{h2_{out_2}}}\frac{\partial{h2_{out_2}}}{\partial{h2_{in_2}}}\frac{\partial{h2_{in_2}}}{\partial{w_{j_1k_2}}} & \frac{\partial{E}}{\partial{h2_{out_3}}}\frac{\partial{h2_{out_3}}}{\partial{h2_{in_3}}}\frac{\partial{h2_{in_3}}}{\partial{w_{j_1k_3}}} \\ \frac{\partial{E}}{\partial{h2_{out_1}}}\frac{\partial{h2_{out_1}}}{\partial{h2_{in_1}}}\frac{\partial{h2_{in_1}}}{\partial{w_{j_2k_1}}} & \frac{\partial{E}}{\partial{h2_{out_2}}}\frac{\partial{h2_{out_2}}}{\partial{h2_{in_2}}}\frac{\partial{h2_{in_2}}}{\partial{w_{j_1k_2}}} & \frac{\partial{E}}{\partial{h2_{out_3}}}\frac{\partial{h2_{out_3}}}{\partial{h2_{in_3}}}\frac{\partial{h2_{in_3}}}{\partial{w_{j_1k_3}}} \\ \frac{\partial{E}}{\partial{h2_{out_1}}}\frac{\partial{h2_{out_1}}}{\partial{h2_{in_1}}}\frac{\partial{h2_{in_1}}}{\partial{w_{j_3k_1}}} & \frac{\partial{E}}{\partial{h2_{out_2}}}\frac{\partial{h2_{out_2}}}{\partial{h2_{in_2}}}\frac{\partial{h2_{in_2}}}{\partial{w_{j_3k_2}}} & \frac{\partial{E}}{\partial{h2_{out_3}}}\frac{\partial{h2_{out_3}}}{\partial{h2_{in_3}}}\frac{\partial{h2_{in_3}}}{\partial{w_{j_3k_3}}} \end{bmatrix}$ $= \begin{bmatrix} \frac{\partial{E}}{\partial{h2_{out_1}}} & \frac{\partial{E}}{\partial{h2_{out_2}}} & \frac{\partial{E}}{\partial{h2_{out_3}}} \\ \frac{\partial{E}}{\partial{h2_{out_1}}} & \frac{\partial{E}}{\partial{h2_{out_2}}} & \frac{\partial{E}}{\partial{h2_{out_3}}} \\ \frac{\partial{E}}{\partial{h2_{out_1}}} & \frac{\partial{E}}{\partial{h2_{out_2}}} & \frac{\partial{E}}{\partial{h2_{out_3}}} \end{bmatrix} \ast \begin{bmatrix} \frac{\partial{h2_{out_1}}}{\partial{h2_{in_1}}} & \frac{\partial{h2_{out_2}}}{\partial{h2_{in_2}}} & \frac{\partial{h2_{out_3}}}{\partial{h2_{in_3}}} \\ \frac{\partial{h2_{out_1}}}{\partial{h2_{in_1}}} & \frac{\partial{h2_{out_2}}}{\partial{h2_{in_2}}} & \frac{\partial{h2_{out_3}}}{\partial{h2_{in_3}}} \\ \frac{\partial{h2_{out_1}}}{\partial{h2_{in_1}}} & \frac{\partial{h2_{out_2}}}{\partial{h2_{in_2}}} & \frac{\partial{h2_{out_3}}}{\partial{h2_{in_3}}} \end{bmatrix} \ast \begin{bmatrix} \frac{\partial{h2_{in_1}}}{\partial{w_{j_1k_1}}} & \frac{\partial{h2_{in_2}}}{\partial{w_{j_1k_2}}} & \frac{\partial{h2_{in_3}}}{\partial{w_{j_1k_3}}} \\ \frac{\partial{h2_{in_1}}}{\partial{w_{j_2k_1}}} & \frac{\partial{h2_{in_2}}}{\partial{w_{j_2k_2}}} & \frac{\partial{h2_{in_3}}}{\partial{w_{j_2k_3}}} \\ \frac{\partial{h2_{in_1}}}{\partial{w_{j_3k_1}}} & \frac{\partial{h2_{in_2}}}{\partial{w_{j_3k_2}}} & \frac{\partial{h2_{in_3}}}{\partial{w_{j_3k_3}}} \end{bmatrix}$